Proof of work

The proof-of-work ‘PoW’ must produce a hash that is less than the target. A higher target means it is less difficult to find a hash that is below the target. A lower target means it is more difficult to find a hash below the target. The target and difficulty are inversely related.

---

What is a SHA256 hash?

With SHA256, the output is always 256 bits long, regardless of the size of the input. For example, we will calculate the SHA256 hash of the phrase, “Hello, World!”:

$ echo "Hello, world!" | sha256sum
d9014c4624844aa5bac314773d6b689ad467fa4e1d1a50a1b8a99d5a95f72ff5  -

---

Rust example of Proof of Work using SHA256

This is inspired by an example on GitHub:

❯ ./solver-single
Usage: ./solver-single <prefix> <difficulty>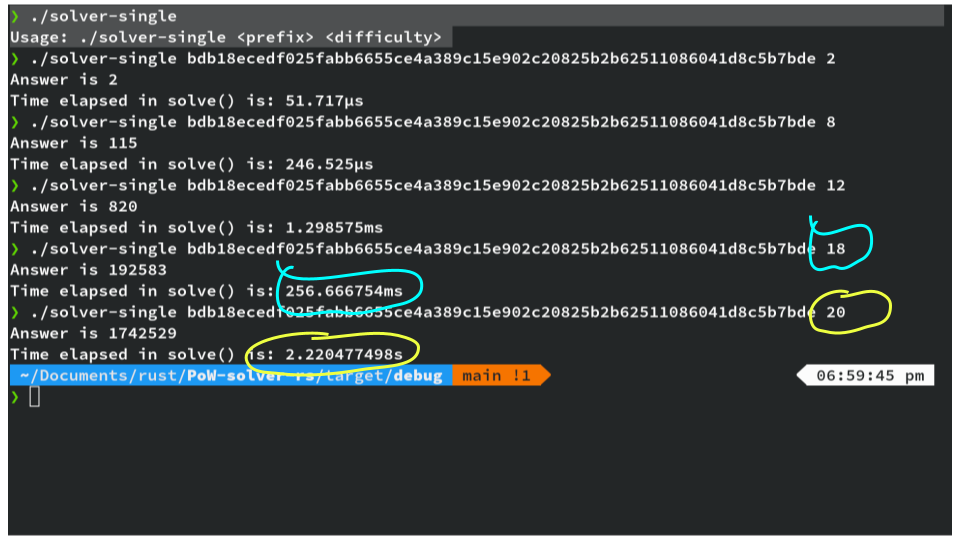

Proof of work using Rust code:

So if you’ve got the gist of what’s been shown above, let’s write some code from bares bones and try and unpick the essential parts that we need.

We’re going to make use of the ring crate for the SHA256 hash function.

ring = "0.17.8"

use std::fmt::Write;

use ring::digest::{Context, SHA256};

Note : https://docs.rs/ring/0.17.8/ring/digest/index.html

If all the data is available in a single contiguous slice then the digest function should be used. Otherwise, the digest can be calculated in multiple steps using Context.

ring documentation

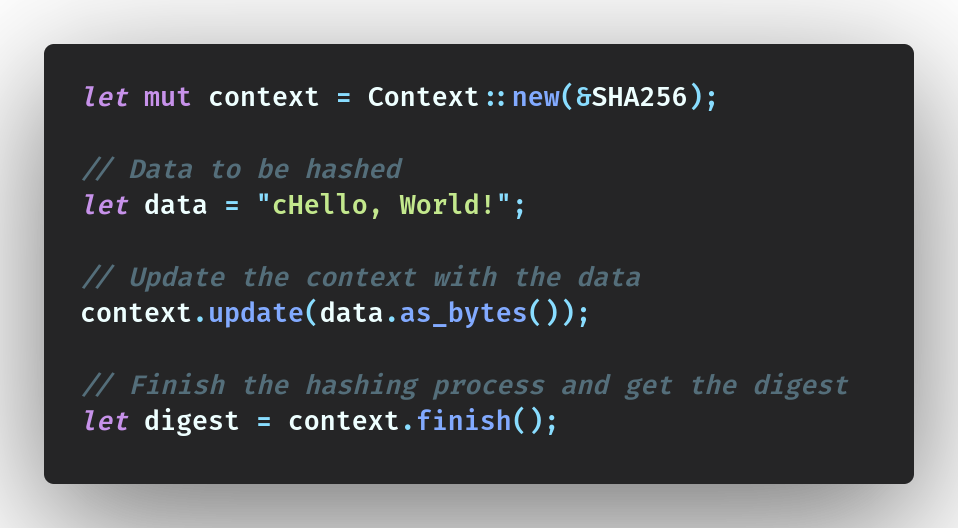
Inside main, we’ll do the hash operation, I am using context here, although as per the documentation, it’s not essential here.

Once we have a hash we check if it has the target number of zeros. I tried putting a, b, and finally c in front of “hello world” and then I got the “0” at the start.

Leading zeros

The leading_zeros() method is then applied to count the number of leading zeros in the binary representation of that integer. The whole point of this code is to find a hash that has more leading zeros (zeros at the start, or at the left, however you wish to call it, it’s the same thing).

The target is to find a number with n number of zeros and then after a few attempts weshould find one.

*different combinations of a letter plus ‘hello world’

Hello world will always give the same hash, that’s why we need to add something different to it each time, so that we can get a new hash, and another chance of getting a zero at the start.

The letter that we add at the start is just for our toy example, in Bitcoin the miners use a “nonce” – number used once, and keep adjusting it until they get the hash with the required number of zeros to match the target specified by the “difficulty”. See below, by adding “something” to our data we can affect the hash.

This can’t be guessed, so it has to be calculated, using processing power and electricity, thus to find the successful hash, you have proof that you did some work…Proof of work!

Steps in proof of work:

(For a Bitcoin style implementation)

• Initialization: Set the target difficulty and initialize a block with transactions.
• Nonce Iteration: Increment a nonce value in the block header.
• Hash Computation: Hash the entire block (including nonce) using a cryptographic hash function.
• Comparison: Compare the computed hash with the target difficulty.
• Condition Check: If the hash meets the difficulty criteria, the proof of work is successful; otherwise, iterate the nonce and repeat.
• Block Validation: Once a valid proof of work is found, the block is considered mined and can be added to the blockchain.

 for &byte in digest.as_ref() {
    write!(&mut actual_hex, "{:02x}", byte).expect("Failed to write hex");
}

This code above is purely for our toy example.

Sure, let’s break down the code:

for &byte in digest.as_ref() {
    write!(&mut actual_hex, "{:02x}", byte).expect("Failed to write hex");
}

This code is part of a loop that goes through each byte in the digest and converts it to a hexadecimal (hex) representation, appending it to the actual_hex string.

Here’s a more detailed explanation:

1. digest.as_ref(): digest is a variable containing some binary data, likely a cryptographic hash. as_ref() converts it into a slice of bytes.
2. for &byte in ...: This is a loop that iterates over each byte in the slice of bytes obtained from digest.as_ref().
3. write!(&mut actual_hex, "{:02x}", byte): Inside the loop, this line uses the write! macro to format each byte (byte) in hexadecimal representation ({:02x}) and appends it to the actual_hex string. The &mut actual_hex indicates that actual_hex is mutable, and it will be modified during each iteration.
4. .expect("Failed to write hex"): The expect method is used to handle errors. If there’s an error during the write operation, this part will print the specified error message (“Failed to write hex”) and terminate the program.

To simplify, this loop is taking each byte of a binary digest, converting it to a two-digit hexadecimal representation, and appending it to a string (actual_hex). The final result is a string containing the hexadecimal representation of the entire digest.

This is commonly done when dealing with cryptographic hashes or binary data that needs to be presented in a human-readable format.

Bitcoin’s proof of work

In the Bitcoin implementation of Proof of Work, once a miner successfully finds a nonce that, when combined with the block data, produces a hash below the target difficulty, the following steps occur:

1. Block Broadcast: The miner broadcasts the newly mined block to the rest of the network.
2. Network Validation: Other nodes in the network independently verify the validity of the proof of work by recalculating the hash using the provided nonce and block data.
3. Consensus: If the majority of the network nodes agree that the proof of work is valid, the block is accepted as legitimate.
4. Block Addition to Blockchain: The newly mined block is added to the blockchain, becoming part of the distributed ledger.
5. Reward Assignment: The miner who successfully mined the block is rewarded with newly created bitcoins (block reward) and any transaction fees associated with the transactions included in the block.

This process ensures the security and decentralization of the blockchain by making it computationally expensive to add blocks, and it provides an incentive for miners to participate in the network.

https://play.rust-lang.org/?version=stable&mode=debug&edition=2021&gist=faf5b9af72fa87cef3ae320f04a8f49f

If you’re interested in exploring Bitcoin with Rust

Calculate the current Bitcoin ‘proof of work’ target for miners

If you have access to a Bitcoin node you can get the current difficulty :

As of 1st March 2024 :

Chain: main
Blocks: 832739
Headers: 832739
Verification progress: 99.9993%
Difficulty: 79351228131136.77

max_target = 0x00000000FFFF0000000000000000000000000000000000000000000000000000
difficulty = 79351228131136.77
target = max_target / difficulty

print(target)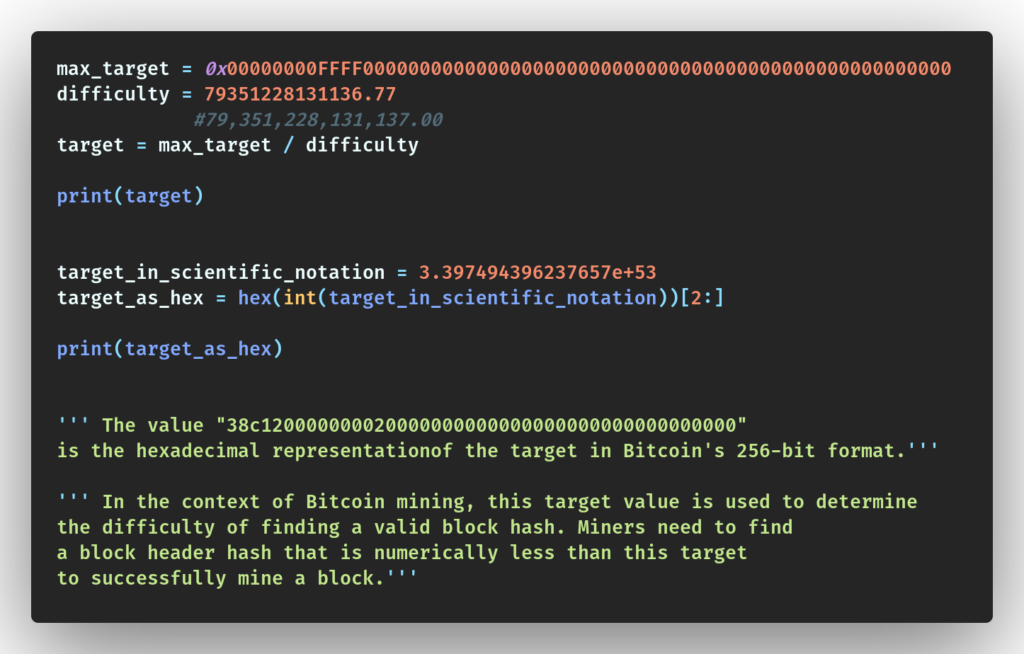

target_in_scientific_notation = 3.397494396237657e+53
target_as_hex = hex(int(target_in_scientific_notation))[2:]

print(target_as_hex)

Verify the result

The result is: “38c120000000020000000000000000000000000000000” which is the hexadecimal representation of the target in Bitcoin’s 256-bit format.

In the context of Bitcoin mining, this target value is used to determine the difficulty of finding a valid block hash.

Miners need to find a block header hash that is numerically less than this target to successfully mine a block.

Remember that the target is adjusted periodically to ensure that blocks are mined at an average rate of one every 10 minutes.

If the network hash rate increases, making block generation too fast, the difficulty adjusts, resulting in a lower target and making it harder to find a valid hash.

Conversely, if the network hash rate decreases, the difficulty adjusts to a higher target, making it easier to find a valid hash.

Proof of work! ✅✅✅

Try my Rust proof of work code in Rust playground

Python code to verify the result : https://gist.github.com/RGGH/e7db6cf0f8898ab3afb56ae05b821913#file-proof_of_work_checker-py

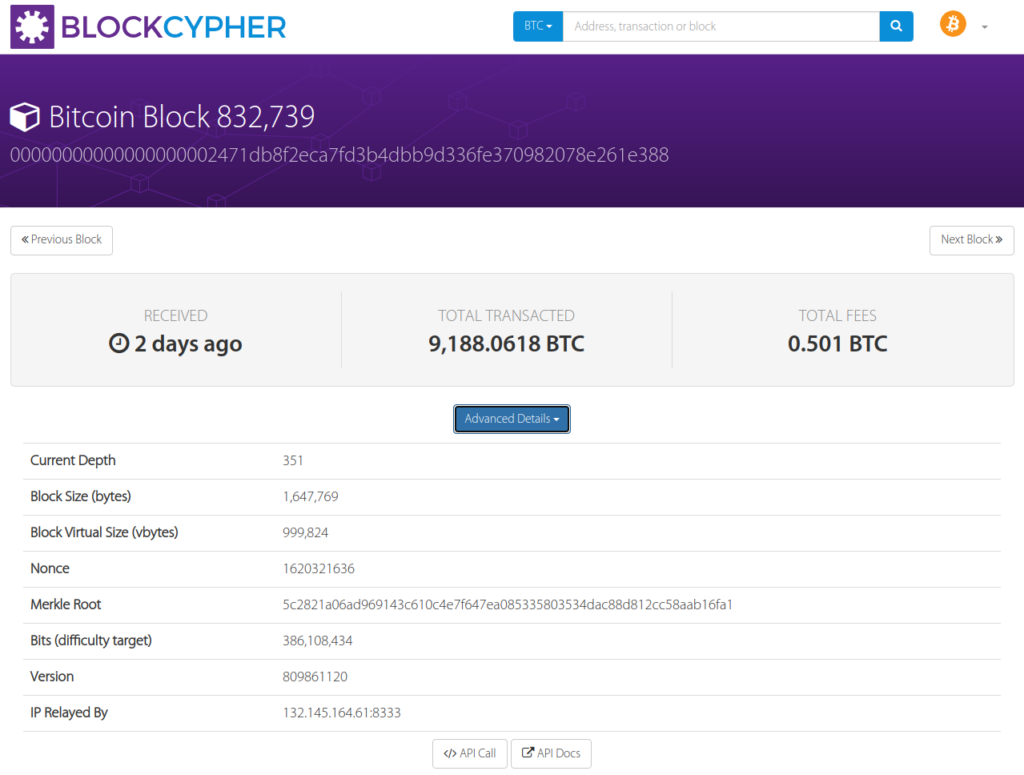
How to get the transaction info from Bitcoin Core ?

bitcoin-cli getblockhash 832739
00000000000000000002471db8f2eca7fd3b4dbb9d336fe370982078e261e388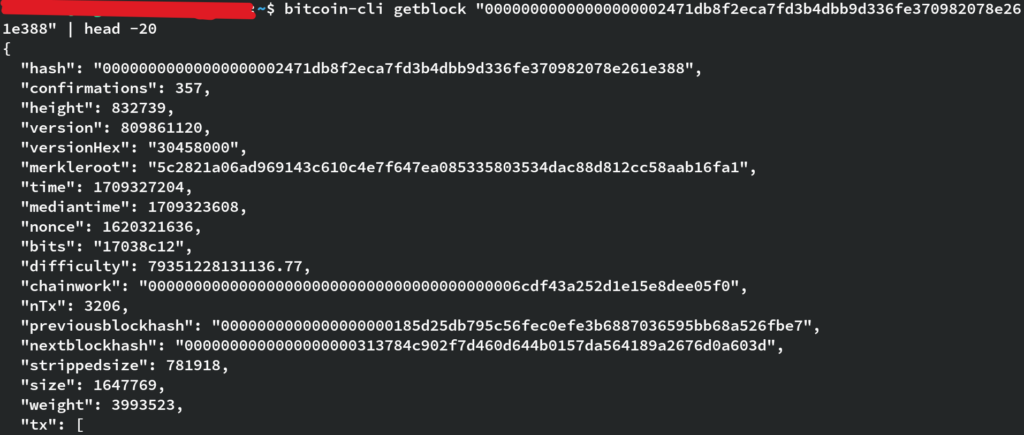

$ bitcoin-cli getblock "00000000000000000002471db8f2eca7fd3b4dbb9d336fe370982078e261e388" | head -20
{
  "hash": "00000000000000000002471db8f2eca7fd3b4dbb9d336fe370982078e261e388",
  "confirmations": 357,
  "height": 832739,
  "version": 809861120,
  "versionHex": "30458000",
  "merkleroot": "5c2821a06ad969143c610c4e7f647ea085335803534dac88d812cc58aab16fa1",
  "time": 1709327204,
  "mediantime": 1709323608,
  "nonce": 1620321636,
  "bits": "17038c12",
  "difficulty": 79351228131136.77,
  "chainwork": "00000000000000000000000000000000000000006cdf43a252d1e15e8dee05f0",
  "nTx": 3206,
  "previousblockhash": "0000000000000000000185d25db795c56fec0efe3b6887036595bb68a526fbe7",
  "nextblockhash": "0000000000000000000313784c902f7d460d644b0157da564189a2676d0a603d",
  "strippedsize": 781918,
  "size": 1647769,
  "weight": 3993523,
  "tx": [

Note, the “bits” and “difficulty” values in the Bitcoin block header are directly linked. The “bits” field is a compact representation of the difficulty target, and the “difficulty” field is the actual difficulty level.

The relationship between the “bits” value and the difficulty level is determined by the Bitcoin protocol. The “bits” value is a 4-byte compact representation that encodes the difficulty target. The difficulty level is then calculated based on this encoded target.

The formula to calculate difficulty from the “bits” value is as follows:

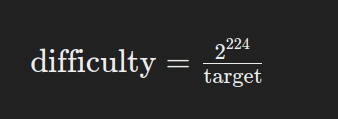
So, as the “bits” value changes, the difficulty level will change accordingly. Miners use the difficulty level to determine the amount of computational effort required to find a valid block hash. The system adjusts the difficulty approximately every two weeks to maintain an average block time of around 10 minutes in the Bitcoin network.