Binary Tree in Python

Let’s create a Binary Tree in Python and understand how it works.

---

Key characteristics of a binary tree include:

1. Root Node: The topmost node of the tree, serving as the starting point for traversing the tree.
2. Parent and Child Nodes: Each node in a binary tree (except the root) has a parent node and may have up to two children nodes. The parent node is the immediate node above the child node.
3. Left and Right Children: Each node can have at most two children, referred to as the left child and the right child. These children nodes are positioned to the left and right of the parent node, respectively.
4. Leaf Nodes: Nodes that do not have any children are called leaf nodes or terminal nodes. They are the nodes at the bottom-most level of the tree.
5. Internal Nodes: Nodes that have at least one child are called internal nodes. They are not leaf nodes and are located somewhere between the root node and the leaf nodes.
6. Depth and Height: The depth of a node is the length of the path from the root node to that node. The height of a node is the length of the longest path from that node to a leaf node. The height of the binary tree is the height of the root node.
7. Binary Search Property: In a binary search tree (a specific type of binary tree), the values stored in the left subtree of a node are less than the value of the node, and the values stored in the right subtree are greater than the value of the node. This property allows for efficient searching, insertion, and deletion operations.

Binary trees are used in various applications such as representing hierarchical data structures, implementing search algorithms like binary search, and serving as the foundation for more complex data structures like binary search trees, AVL trees, and red-black trees.

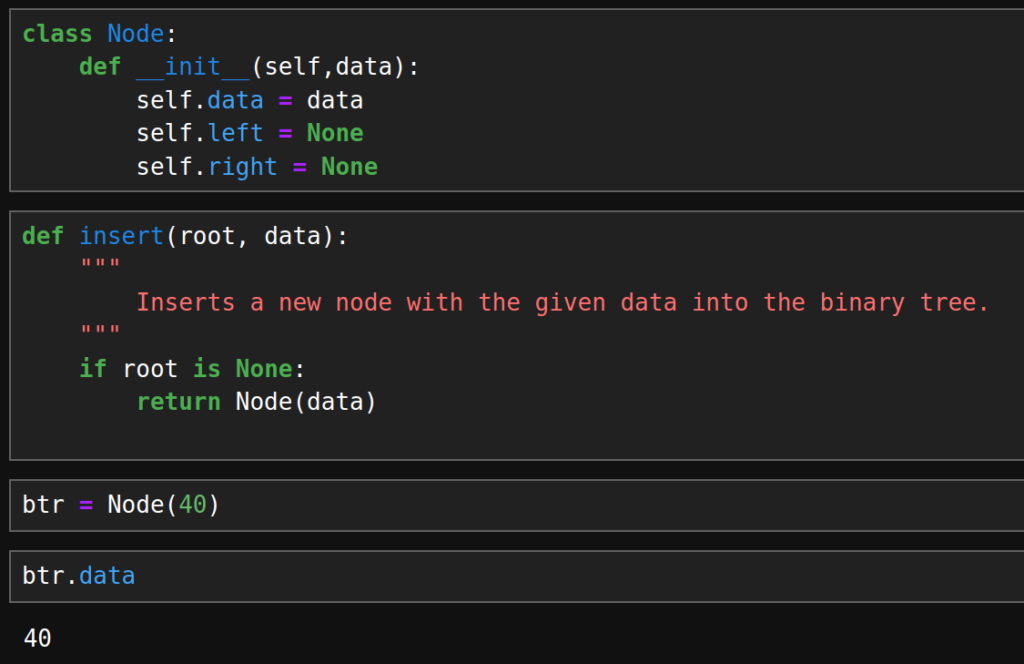
Code for a Binary Tree

class Node:
  """
  A node class representing a single element in the binary tree.
  """
  def __init__(self, data):
    self.data = data
    self.left = None  # Left child
    self.right = None  # Right child

def insert(root, data):
  """
  Inserts a new node with the given data into the binary tree.
  """
  if root is None:
    return Node(data)
  if data < root.data:
    root.left = insert(root.left, data)
  else:
    root.right = insert(root.right, data)
  return root

def inorder_traversal(root):
  """
  Performs an in-order traversal of the binary tree, printing data.
  """
  if root is not None:
    inorder_traversal(root.left)
    print(root.data, end=" ")
    inorder_traversal(root.right)

# Example usage
root = None
root = insert(root, 50)
insert(root, 30)
insert(root, 20)
insert(root, 40)
insert(root, 70)
insert(root, 60)

print("Inorder traversal: ")
inorder_traversal(root)

    50

    50
   /
  30

    50
   /
  30
 /
20

    50
   /
  30
 /  \
20  40

    50
   /  \
  30   70
 /  \
20  40

    50
   /  \
  30   70
 /  \ /
20  40 60

      50
     /   \
    30    70
   /  \  /  
  20  40 60
  /        
 10