What is Candle?
CANDLE Handles all the heavy mathematical lifting – matrix multiplications, softmax, broadcasting, gradients, and hardware acceleration. Think of it like “NumPy” for AI, for Rust!
Candle lets you run ML models entirely inside a Rust program, without Python or a separate service like Ollama.
The Magic: When you write something like q.matmul(&k.t())?.softmax(D::Minus1)?, CANDLE automatically:
- Optimizes the matrix multiplication for your hardware
- Handles memory layout efficiently
- Computes gradients for backprop
- Uses CUDA/Metal if available
So you get to think at the algorithm level (attention mechanisms, residuals) while CANDLE handles the implementation level (optimized tensor ops, hardware acceleration).
It’s like having a really smart math co-pilot that lets you focus on the AI architecture instead of worrying about BLAS libraries and GPU kernels! 🦀
“Candle is a minimalist ML framework for Rust with a focus on performance (including GPU support) and ease of use. “
Try the online demos: whisper, LLaMA2, T5, yolo, Segment Anything.
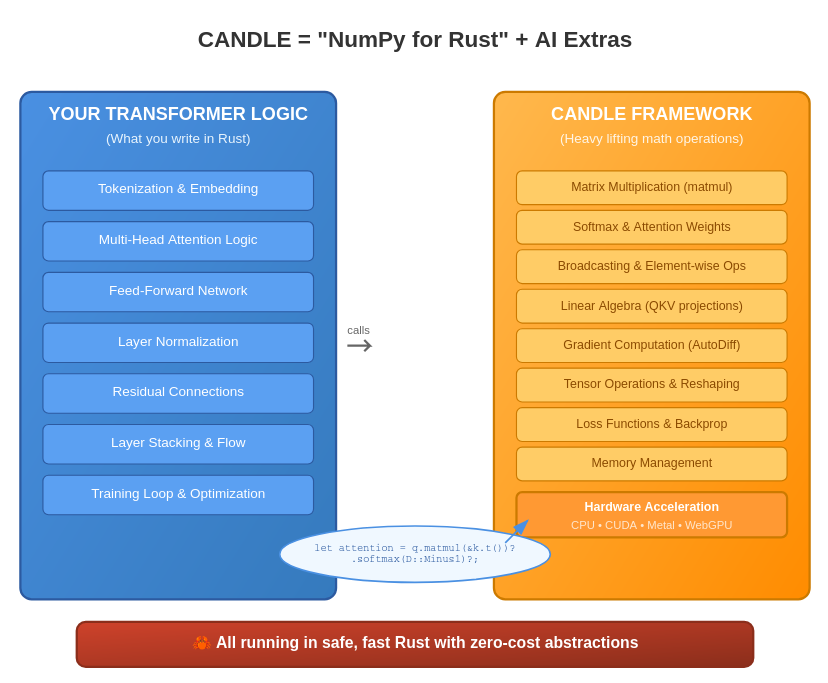
CANDLE is specifically designed for building LLMs from scratch
What CANDLE gives you for LLM building:
Core LLM Components:
- ✅ Transformer layers (attention, feed-forward, layer norm)
- ✅ Tokenization (built-in support for common tokenizers)
- ✅ Embeddings (token + positional embeddings)
- ✅ Autoregressive generation (sampling, beam search, etc.)
- ✅ Training infrastructure (optimizers, loss functions, checkpointing)
Advanced Features:
- ✅ Memory-efficient attention (flash attention, sparse attention)
- ✅ Model parallelism (split large models across GPUs)
- ✅ Quantization (run models in 4-bit, 8-bit)
- ✅ ONNX/SafeTensors support (load existing models)
Real Examples:
People have already built full LLMs with CANDLE:
- Llama 2/3 implementations
- GPT-style models
- Mistral/Mixtral models
- Custom architectures

What is ReLu?
ReLU (Rectified Linear Unit) is one of the most popular activation functions in neural networks. It’s super simple:
The Function:
ReLU(x) = max(0, x)
Translation: If the input is positive, keep it. If negative, make it zero.
Visually:
Input: [-2, -1, 0, 1, 2, 3]
Output: [ 0, 0, 0, 1, 2, 3]
Why It’s Everywhere:
✅ Advantages:
- Simple to compute (just
max(0, x)) - Fast gradient (derivative is either 0 or 1)
- Fixes vanishing gradients (doesn’t squash values like sigmoid)
- Sparse activations (many neurons output 0, saves computation)
❌ Disadvantages:
- “Dying ReLU” problem (neurons can get stuck outputting 0)
- Not differentiable at x=0 (but works fine in practice)
- Unbounded output (can grow very large)
In Practice:
Before ReLU:
// Hidden layer outputs: [-0.5, 2.3, -1.2, 0.8]
After ReLU:
// Activated outputs: [0.0, 2.3, 0.0, 0.8]
ReLU Variants:
- Leaky ReLU:
max(0.01x, x)(small slope for negatives) - ELU: Exponential version for smoother gradients
- GELU: Gaussian-based (used in transformers like GPT)
Fun fact: ReLU was a game-changer that helped enable deep learning by solving gradient problems that plagued earlier activation functions! 🚀
What is Feed FORWARD?
Why it exists
- Attention captures relationships between tokens.
- Feed-forward captures nonlinear transformations of each token individually, allowing richer feature extraction.
Think of it like:
- Attention: “how does each word relate to every other word?”
- Feed-forward: “given the representation of this word, how can I transform it into a more expressive embedding?”
Structure: Linear → Activation → Dropout → Linear
- Weights1 & Bias1: Project to larger dimension (usually 4x bigger)
- Activation: Add non-linearity (ReLU/GELU/SwiGLU)
- Dropout: Randomly zero neurons (prevents overfitting)
- Weights2 & Bias2: Project back to original dimension
In Transformers Specifically:
Typical dimensions:
- Input:
[batch, seq_len, 768] - After first linear:
[batch, seq_len, 3072](4x expansion) - After second linear:
[batch, seq_len, 768](back to original)
Modern variants:
- SwiGLU: Uses gated activation instead of ReLU
- RMSNorm: Sometimes replaces layer norm
- No bias: Many recent models skip bias terms
So yes – weights, biases, and dropout are all there, but the key insight is it’s a two-step expand-then-compress operation! 🎯

