Bitcoin Scripts and Script Language

Bitcoin Script is a powerful and unique scripting language at the heart of the Bitcoin blockchain, defining the rules governing transaction execution. Designed by Satoshi Nakamoto, it enables users to create complex, programmable transactions, unlocking a realm of possibilities beyond simple peer-to-peer transfers. Let’s look at the basics of how it works…

Successful Basic Script and Assembly equivalent:

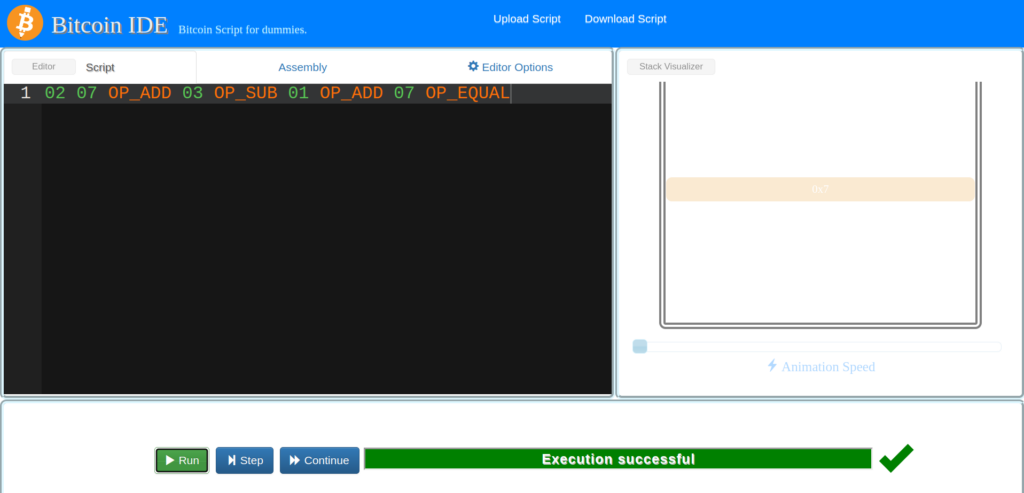
Reference :

https://siminchen.github.io/bitcoinIDE/build/editor.html#

https://learn.saylor.org/mod/book/view.php?id=36364&chapterid=18952

02 07 OP_ADD 03 OP_SUB 01 OP_ADD 07 OP_EQUAL

0102010793010394010193010787

You can just as easily paste in this “Assembly”and execute it as you can the Script.

Obviously the script is easier for a human to create.

---

Transaction Scripts

If the unlocking script is executed without errors (e.g., it has no “dangling” pointers left over), the main stack is copied and the locking script is executed

CS120: Bitcoin for Developers 

See : https://learn.saylor.org/mod/book/view.php?id=36364&chapterid=18952

OP_CHECKSIG is perhaps the most interesting part of the process:

The OP_CHECKSIG operation checks if the digital signature matches the public key provided in the transaction. If they match, it means the person spending the Bitcoin(s) is the rightful owner of the associated private key. Have a play around using https://ide.scriptwiz.app/

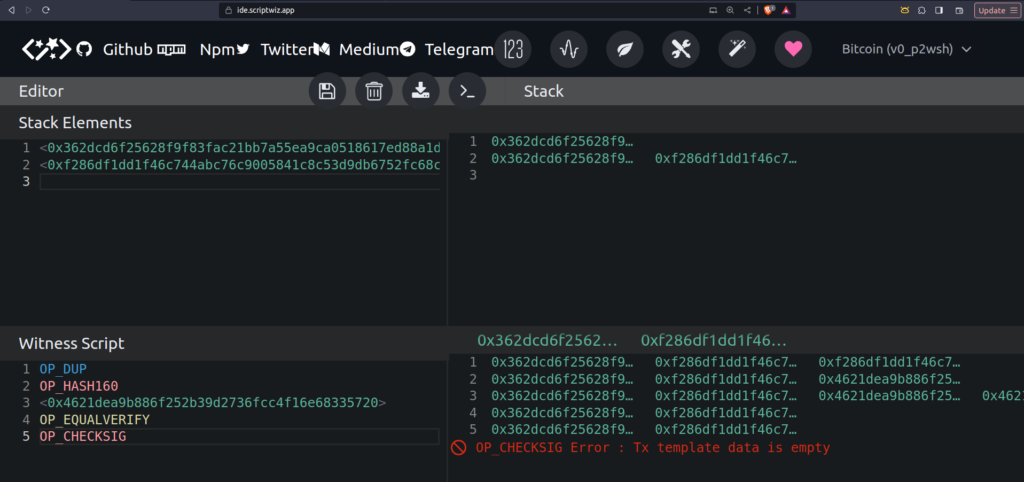
When we say a signature is “valid,” it means that the signature was indeed created by the private key corresponding to the public key in the transaction. In other words, the signature can be successfully verified using the public key, confirming that the person initiating the transaction is indeed the owner of the private key associated with that public key.

So, as long as you have the digital signature and the corresponding public key, you can verify the authenticity of the signature and confirm ownership of the private key.

Verify the owner

from ecdsa import SigningKey, SECP256k1

# Generate a private key
private_key = SigningKey.generate(curve=SECP256k1)

# Get the corresponding public key
public_key = private_key.get_verifying_key()

# Create a message to sign
message = b"Hello, World!"

# Sign the message
signature = private_key.sign(message)

signature_string = signature.hex()
print(f"Signature: \n{signature_string}\n")

# Assuming 'public_key' is the bytes object
public_key_string = public_key.to_string().hex()
print(f"Public key: \n{public_key_string}")


# Verify the signature - ensure you pass the message that was signed!
if public_key.verify(signature, message):
    print("\nSignature is valid.")
else:
    print("Signature is not valid.")

Signature: 
0ec65fae53ed23988e19331c7873b2dc738c0b364588be1519cd2435c2eb5a32f2e863993daf256188b5930fac59b10c82f16055c206f98d68dc12a39a026d0e

Public key: 
0ec65fae53ed23988e19331c7873b2dc738c0b364588be1519cd2435c2eb5a32f2e863993daf256188b5930fac59b10c82f16055c206f98d68dc12a39a026d0e

Signature is valid.

The raw public key and signature are not directly compared in Bitcoin scripts. Instead, the public key is hashed, and the hash is compared against a pre-determined hash. If they match, the script proceeds to the signature verification.

Modern Bitcoin addresses and transactions use compressed public keys for efficiency and smaller transaction sizes. This is done to save space on the blockchain and reduce transaction fees.

https://bitcoin.stackexchange.com/a/90417/139723

use secp256k1::{Message, PublicKey, Secp256k1, SecretKey};

fn main() {
    let secp = Secp256k1::new();
    let secret_key = SecretKey::from_slice(&[0xcd; 32]).expect("32 bytes, within curve order");
    let public_key = PublicKey::from_secret_key(&secp, &secret_key);
    let message = Message::from_digest_slice(&[0xab; 32]).expect("32 bytes");

    let sig = secp.sign_ecdsa(&message, &secret_key);
    assert!(secp.verify_ecdsa(&message, &sig, &public_key).is_ok());
}

This Rust code demonstrates how to use the secp256k1 crate to perform Elliptic Curve Digital Signature Algorithm (ECDSA) operations. ECDSA is commonly used in blockchain and cryptography for creating and verifying digital signatures.

Here’s a breakdown of the code:

1. Import the necessary items from the secp256k1 crate: use secp256k1::{Message, PublicKey, Secp256k1, SecretKey}; This brings into scope the types and methods needed for working with the secp256k1 elliptic curve.
2. Define the main function: fn main() { // ... } This is the entry point of the Rust program.
3. Create a new instance of the Secp256k1 struct: let secp = Secp256k1::new(); This initializes a new secp256k1 context, which is necessary for other cryptographic operations.
4. Generate a secret key: let secret_key = SecretKey::from_slice(&[0xcd; 32]).expect("32 bytes, within curve order"); A 32-byte secret key is created here. The key is generated from a slice containing the byte 0xcd repeated 32 times. The expect method is used to handle any errors that might occur during the key generation.
5. Derive the corresponding public key from the secret key: let public_key = PublicKey::from_secret_key(&secp, &secret_key); This computes the corresponding public key using the secp256k1 elliptic curve parameters.
6. Create a message: let message = Message::from_digest_slice(&[0xab; 32]).expect("32 bytes"); A 32-byte message is created using the Message::from_digest_slice method. The message content is generated from a slice containing the byte 0xab repeated 32 times.
7. Sign the message using the secret key: let sig = secp.sign_ecdsa(&message, &secret_key); The sign_ecdsa method is used to generate a digital signature for the given message using the provided secret key.
8. Verify the signature: assert!(secp.verify_ecdsa(&message, &sig, &public_key).is_ok()); The verify_ecdsa method is used to verify the signature against the original message and public key. If the verification is successful, the result will be Ok, and the assert! macro will succeed, indicating that the signature is valid.

In summary, this code demonstrates the basic process of generating a secp256k1 key pair, signing a message with the private key, and then verifying the signature using the corresponding public key and original message.

Note: In a real-world scenario, you would typically use a secure method to generate a random secret key rather than using a constant value as shown in the example. The use of a constant value is for demonstration purposes only.

https://docs.rs/secp256k1/latest/secp256k1/

In a real-world scenario, when signing a Bitcoin transaction, you don’t typically sign an arbitrary message like “hello.” Instead, you sign the transaction itself. The transaction includes information such as the transaction inputs, outputs, and other necessary details. This ensures that the signature is specific to that particular transaction, preventing it from being reused for a different purpose.