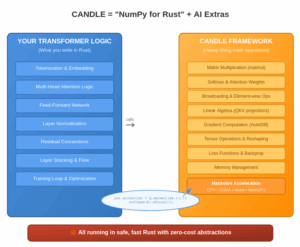
ReLU – Rectified Linear Unit
What is x.max(0.0)?
x.max(0.0) returns the maximum value between x and 0.0. It’s Rust’s method for finding the larger of two numbers.
ReLU Worked Examples:
ReLU (Rectified Linear Unit) formula: ReLU(x) = max(0, x)
This means:
- If
xis positive → keep it - If
xis negative → replace with 0
Here are concrete examples:
// Positive inputs - pass through unchanged
relu(5.0) = 5.0.max(0.0) = 5.0 ✓ (5.0 > 0)
relu(2.3) = 2.3.max(0.0) = 2.3 ✓ (2.3 > 0)
relu(0.01) = 0.01.max(0.0) = 0.01 ✓ (0.01 > 0)
// Zero - stays zero
relu(0.0) = 0.0.max(0.0) = 0.0 ✓ (equal)
// Negative inputs - clamped to zero
relu(-3.0) = -3.0.max(0.0) = 0.0 ✓ (0 > -3.0)
relu(-0.5) = -0.5.max(0.0) = 0.0 ✓ (0 > -0.5)
relu(-100.0)= -100.0.max(0.0)=0.0 ✓ (0 > -100.0)
Visual Example:
Input: -3 -2 -1 0 1 2 3
↓ ↓ ↓ ↓ ↓ ↓ ↓
ReLU: 0 0 0 0 1 2 3
└───┴───┴───┘ (killed negative values)
└───┴───┴───┘ (kept positive values)
Why ReLU is Powerful:
- Simple: Just one comparison!
- Fast: No expensive exponentials like sigmoid
- Non-linear: Creates the “bend” at x=0
- No vanishing gradient: For positive x, gradient = 1 (unlike sigmoid which saturates)
Comparison with Sigmoid:
sigmoid(-2.0) = 0.119 // Smooth curve, never zero
relu(-2.0) = 0.0 // Hard cutoff at zero
sigmoid(2.0) = 0.881 // Bounded to (0,1)
relu(2.0) = 2.0 // Unbounded above
ReLU is like a one-way gate: it lets positive signals through but blocks negative ones completely!
Usage:
// =============================================================================
// NON-LINEAR NEURAL NETWORK: Clean, Modular Implementation
// =============================================================================
type Vector = Vec<f64>;
// =============================================================================
// CORE MATHEMATICAL OPERATIONS
// =============================================================================
fn dot_product(v1: &[f64], v2: &[f64]) -> Option<f64> {
if v1.len() != v2.len() {
return None;
}
Some(v1.iter().zip(v2.iter()).map(|(a, b)| a * b).sum())
}
// =============================================================================
// ACTIVATION FUNCTIONS
// =============================================================================
fn sigmoid(x: f64) -> f64 {
1.0 / (1.0 + (-x).exp())
}
fn sigmoid_derivative(x: f64) -> f64 {
let s = sigmoid(x);
s * (1.0 - s)
}
#[allow(dead_code)]
fn relu(x: f64) -> f64 {
x.max(0.0)
}
#[allow(dead_code)]
fn relu_derivative(x: f64) -> f64 {
if x > 0.0 { 1.0 } else { 0.0 }
}
// =============================================================================
// NEURAL NETWORK MODEL
// =============================================================================
struct NeuralNetwork {
weights: Vector,
learning_rate: f64,
}
impl NeuralNetwork {
fn new(input_size: usize, learning_rate: f64) -> Self {
Self {
weights: vec![0.3; input_size],
learning_rate,
}
}
fn forward(&self, input: &[f64]) -> (f64, f64) {
let z = dot_product(&self.weights, input).expect("Vector size mismatch");
let y_pred = sigmoid(z);
(z, y_pred)
}
fn compute_loss(&self, data: &[(Vector, f64)]) -> f64 {
let mut total_loss = 0.0;
for (x, y_true) in data {
let (_, y_pred) = self.forward(x);
let error = y_true - y_pred;
total_loss += error.powi(2);
}
total_loss / data.len() as f64
}
fn train_epoch(&mut self, data: &[(Vector, f64)]) -> f64 {
let mut gradient_sum = vec![0.0; self.weights.len()];
let mut total_loss = 0.0;
for (x, y_true) in data {
let (z, y_pred) = self.forward(x);
let error = y_true - y_pred;
total_loss += error.powi(2);
let dloss_dy = -2.0 * error;
let dy_dz = sigmoid_derivative(z);
for (i, &x_i) in x.iter().enumerate() {
gradient_sum[i] += dloss_dy * dy_dz * x_i;
}
}
let n = data.len() as f64;
for i in 0..self.weights.len() {
self.weights[i] -= self.learning_rate * gradient_sum[i] / n;
}
total_loss / n
}
fn predict(&self, input: &[f64]) -> f64 {
self.forward(input).1
}
fn get_weights(&self) -> &[f64] {
&self.weights
}
}
// =============================================================================
// DATA GENERATION
// =============================================================================
fn generate_training_data() -> Vec<(Vector, f64)> {
vec![
(vec![0.0, 0.0], 0.500),
(vec![1.0, 0.0], 0.622),
(vec![0.0, 1.0], 0.818),
(vec![1.0, 1.0], 0.881),
(vec![2.0, 0.0], 0.731),
(vec![0.0, 2.0], 0.953),
(vec![2.0, 2.0], 0.982),
(vec![-1.0, 0.0], 0.378),
(vec![0.0, -1.0], 0.182),
(vec![3.0, 1.0], 0.953),
]
}
fn generate_test_data() -> Vec<(Vector, f64)> {
vec![
(vec![1.5, 1.5], 0.953),
(vec![0.5, 0.5], 0.731),
(vec![-1.0, -1.0], 0.047),
]
}
// =============================================================================
// TRAINING FUNCTION
// =============================================================================
fn train_model(
model: &mut NeuralNetwork,
training_data: &[(Vector, f64)],
max_epochs: usize,
convergence_threshold: f64,
) -> usize {
for epoch in 1..=max_epochs {
let loss = model.train_epoch(training_data);
if epoch == 1 || epoch % 500 == 0 {
let w = model.get_weights();
println!(
"Epoch {:4} | Avg Loss: {:.6} | Weights: [{:.4}, {:.4}]",
epoch, loss, w[0], w[1]
);
}
if loss < convergence_threshold {
println!("\n✅ Converged at epoch {}", epoch);
return epoch;
}
}
max_epochs
}
// =============================================================================
// EVALUATION FUNCTIONS
// =============================================================================
fn evaluate_model(model: &NeuralNetwork, test_data: &[(Vector, f64)]) {
println!("\n🧪 GENERALIZATION TEST:");
println!("{}", "-".repeat(63));
let mut total_error = 0.0;
for (i, (x, y_true)) in test_data.iter().enumerate() {
let y_pred = model.predict(x);
let error = (y_true - y_pred).abs();
total_error += error;
let status = if error < 0.05 { "✅" } else { "⚠️" };
println!(
" Test {} {} | Input: {:?} | Pred: {:.4} | True: {:.4} | Error: {:.4}",
i + 1,
status,
x,
y_pred,
y_true,
error
);
}
let avg_error = total_error / test_data.len() as f64;
println!("{}", "-".repeat(63));
println!(" Average error: {:.4}", avg_error);
if avg_error < 0.05 {
println!("\n✅ SUCCESS! Model learned the non-linear pattern!");
}
}
fn compare_linear_nonlinear(model: &NeuralNetwork) {
println!("\n📊 COMPARING LINEAR vs NON-LINEAR:\n");
let test_inputs = vec![
vec![-2.0, 0.0],
vec![-1.0, 0.0],
vec![0.0, 0.0],
vec![1.0, 0.0],
vec![2.0, 0.0],
vec![3.0, 0.0],
];
println!(" Input | Linear Output | Non-Linear (Sigmoid)");
println!(" {}", "-".repeat(55));
for x in test_inputs {
let (z, sigmoid_output) = model.forward(&x);
println!(" {:?} | {:.4} | {:.4}", x, z, sigmoid_output);
}
println!("\n Notice: Linear can go negative or > 1!");
println!(" Sigmoid always stays in (0, 1) - creates curve!\n");
}
// =============================================================================
// DISPLAY FUNCTIONS
// =============================================================================
fn print_header() {
println!("\n╔═══════════════════════════════════════════════════════════════╗");
println!("║ NON-LINEAR NEURAL NETWORK: The Power of Activation ║");
println!("╚═══════════════════════════════════════════════════════════════╝\n");
}
fn print_problem_description(training_data: &[(Vector, f64)]) {
println!("📊 NON-LINEAR PROBLEM:");
println!(" True function: y = sigmoid(0.5*x1 + 1.5*x2)");
println!(" Note: Output is always between 0 and 1 (sigmoid range)\n");
println!(" Training examples: {}", training_data.len());
for (i, (x, y)) in training_data.iter().take(5).enumerate() {
println!(" Example {}: {:?} → {:.3}", i + 1, x, y);
}
println!(" ... and {} more", training_data.len() - 5);
}
fn print_results(model: &NeuralNetwork, final_epoch: usize) {
let correct_weights = vec![0.5, 1.5];
println!("\n{}\n", "=".repeat(63));
println!("🎓 TRAINING COMPLETE! (epoch {})\n", final_epoch);
println!("📈 Results:");
let w = model.get_weights();
println!(" Learned weights: [{:.4}, {:.4}]", w[0], w[1]);
println!(
" Correct weights: [{:.4}, {:.4}]",
correct_weights[0], correct_weights[1]
);
}
fn print_insights() {
println!("╔═══════════════════════════════════════════════════════════════╗");
println!("║ WHY ACTIVATION FUNCTIONS MATTER ║");
println!("╠═══════════════════════════════════════════════════════════════╣");
println!("║ 1. LINEAR MODEL: Can only learn straight lines/planes ║");
println!("║ - No matter how many layers you stack! ║");
println!("║ ║");
println!("║ 2. NON-LINEAR MODEL: Can learn curves and complex patterns ║");
println!("║ - Sigmoid, ReLU, tanh create the 'bends' in the curve ║");
println!("║ ║");
println!("║ 3. UNIVERSAL APPROXIMATION: With activation functions, ║");
println!("║ neural networks can approximate ANY continuous function! ║");
println!("║ ║");
println!("║ 4. BACKPROP CHANGES: Need to include activation derivative ║");
println!("║ in the chain rule (that's the dy_dz term!) ║");
println!("╚═══════════════════════════════════════════════════════════════╝\n");
}
// =============================================================================
// MAIN
// =============================================================================
fn main() {
const LEARNING_RATE: f64 = 0.1;
const MAX_EPOCHS: usize = 5000;
const CONVERGENCE_THRESHOLD: f64 = 1e-5;
print_header();
let training_data = generate_training_data();
let test_data = generate_test_data();
print_problem_description(&training_data);
let mut model = NeuralNetwork::new(2, LEARNING_RATE);
println!("\n🎯 Starting weights: {:?}", model.get_weights());
println!(" Goal weights: [0.5000, 1.5000]\n");
println!("{}\n", "=".repeat(63));
let final_epoch = train_model(&mut model, &training_data, MAX_EPOCHS, CONVERGENCE_THRESHOLD);
print_results(&model, final_epoch);
evaluate_model(&model, &test_data);
compare_linear_nonlinear(&model);
print_insights();
}