Learning with AI (Calculus)
Revisiting A’ Level Maths – Calculus with the help of AI

🔢 What is Calculus?
Calculus is the branch of mathematics that studies change. It has two big halves:
1. Differential Calculus
- Focus: Rates of change, slopes of curves
- Main tool: Derivatives
- Examples:
- “How fast is something changing right now?”
- “What’s the steepness (gradient) at this exact point?”
2. Integral Calculus
- Focus: Accumulation, area under curves
- Main tool: Integrals
- Examples:
- “How much total distance was covered?”
- “What’s the area under this curve?”
- “Add up infinitely small parts”
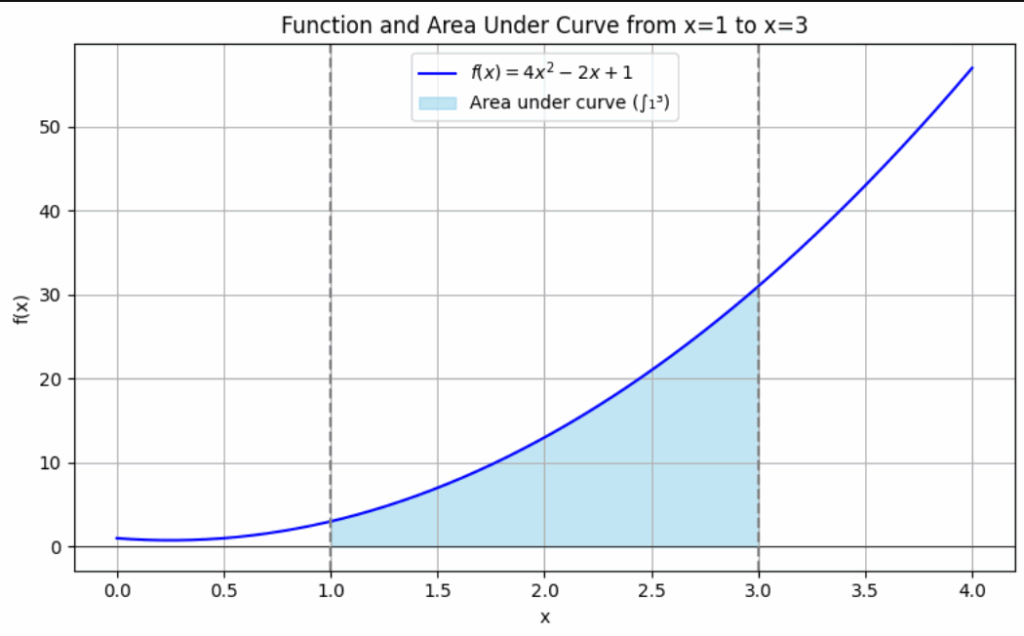
Bonus: They’re Connected!
They’re two sides of the same coin — and the Fundamental Theorem of Calculus links them.
It basically says:
Differentiation undoes integration, and
Integration undoes differentiation.
But in real life? Here’s where stuff like that can pop up:
✅ 1. Area/Volume Problems

✅ 2. Cost or Revenue Models

Again, if you want rate of change of revenue, take the derivative.
✅ 3. Motion with Variable Forces
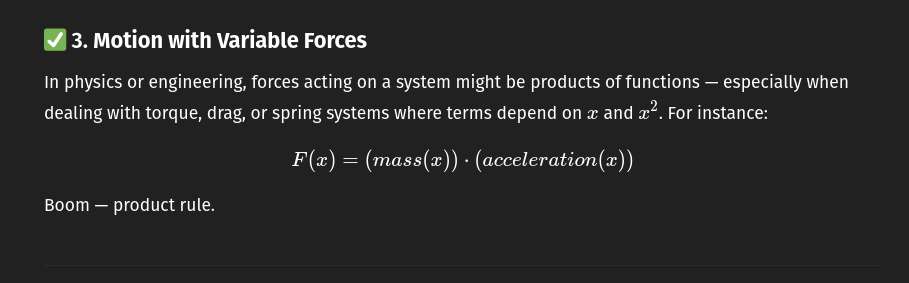
Boom — product rule.
Bottom Line:
A lot of textbook examples are engineered for practice — but in real-world modeling, product rule shows up naturally when two varying things are multiplied.



Example
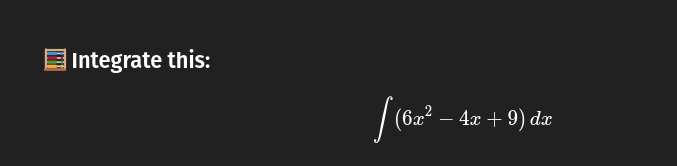
Answer:
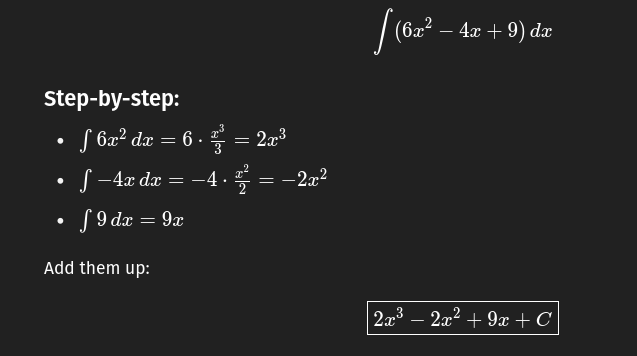
Notatation:


Calculus with code:
Calculus with code uses regular ASCII to represent derivatives and integrals. For derivatives, functions like f(x) = x**2 can be differentiated manually or symbolically using tools like SymPy in Python: diff(f(x), x).
For numerical differentiation, we approximate slopes using: (f(x+h) - f(x)) / h. Integrals can be written as ∫ f(x) dx, but in code we use integrate(f(x), x) for symbolic or use numerical methods like Riemann sums or Simpson’s rule.
ASCII syntax like ** for powers and lambda x: for anonymous functions makes coding calculus readable and practical without needing special math symbols.
Here's some simple Python code using SymPy, a symbolic math library, to compute the derivative using just ASCII:
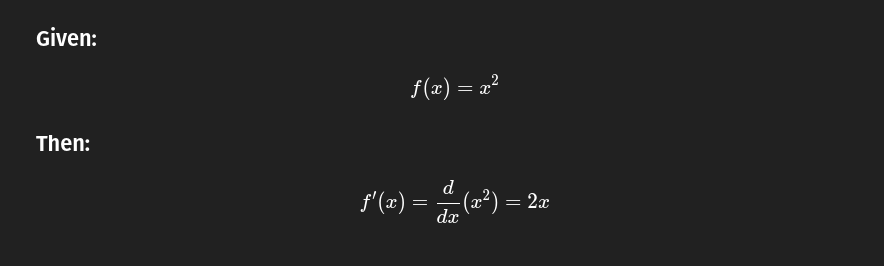
from sympy import symbols, diff
# Define the variable
x = symbols('x')
# Define the function
f = x**2
# Compute the derivative
f_prime = diff(f, x)
# Print results
print("f(x) =", f)
print("f'(x) =", f_prime)
f(x) = x**2
f'(x) = 2*x
Next, find the area between 2 parabolas – see if you can do this in code?
Try solve this using code and then come back and check the answer!
📐 Area Between Two Parabolas
🎯 Given Functions:
Find: The area between these curves using integration
🔍 Step-by-Step Solution:
Set f(x) = g(x):
-x² + 5 = x² – 3
-x² – x² = -3 – 5
-2x² = -8
x² = 4
x = -2 and x = 2
Between x = -2 and x = 2, check at x = 0:
f(0) = -0² + 5 = 5
g(0) = 0² – 3 = -3
So f(x) is above g(x) in this interval.
Area = ∫-22 [f(x) – g(x)] dx
= ∫-22 [(-x² + 5) – (x² – 3)] dx
= ∫-22 [-x² + 5 – x² + 3] dx
= ∫-22 [-2x² + 8] dx
∫ [-2x² + 8] dx = -2x³/3 + 8x + C
Area = [-2x³/3 + 8x]-22
= [-2(2)³/3 + 8(2)] – [-2(-2)³/3 + 8(-2)]
= [-16/3 + 16] – [16/3 – 16]
= [-16/3 + 48/3] – [16/3 – 48/3]
= [32/3] – [-32/3]
= 32/3 + 32/3 = 64/3
Integration limits: x = -2 to x = 2
📝 Key Takeaways:
• The intersection points gave us integer limits: -2 and 2
• We subtracted the lower function from the upper function
• The integral ∫-22 [-2x² + 8] dx gave us the exact area
• This demonstrates how subtracting integrals finds the area between curves