Understanding Merkle Trees in Python: A Step-by-Step Guide
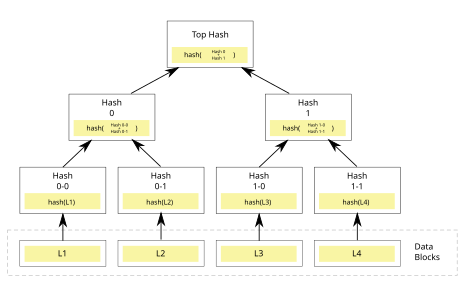
In cryptography and computer science, a hash tree or Merkle tree is a tree in which every “leaf” node is labelled with the cryptographic hash of a data block, and every node that is not a leaf (called a branch, inner node, or inode) is labelled with the cryptographic hash of the labels of its child nodes. A hash tree allows efficient and secure verification of the contents of a large data structure. A hash tree is a generalization of a hash list and a hash chain.

In this article, we will explore the concept of Merkle Trees, their significance in cryptography, and how to implement one in Python. Merkle trees are commonly used in blockchain technologies to efficiently verify the integrity of large datasets.
What is a Merkle Tree?
A Merkle tree is a binary tree where:
- Each leaf node represents the hash of data.
- Non-leaf nodes represent the hash of their child nodes.
- The root node is a hash representing the entire tree.
The advantage of using Merkle trees is that you can verify the integrity of any part of the dataset by only checking a small part of the tree, making it computationally efficient.
How Does a Merkle Tree Work?
- Leaves: The leaves of the tree represent the hashes of the data items.
- Internal Nodes: Each non-leaf node is the hash of its two child nodes.
- Root Hash: The top node of the tree is the Merkle root, a single hash that represents the entire dataset.
Example of a Merkle Tree Implementation in Python
Below is a Python implementation of a Merkle tree:
import hashlib
def hash_data(data):
"""Hashes the input data using SHA-256"""
return hashlib.sha256(data.encode('utf-8')).hexdigest()
def merkle_tree(leaves):
"""Generates a Merkle Tree and returns the root hash"""
# Hash the leaves to create the first level of the tree
layer = [hash_data(leaf) for leaf in leaves]
# Build the tree upwards
while len(layer) > 1:
# Pair up the nodes and hash them together
if len(layer) % 2 != 0: # If there's an odd number, duplicate the last element
layer.append(layer[-1])
# Hash each pair of nodes
layer = [hash_data(layer[i] + layer[i + 1]) for i in range(0, len(layer), 2)]
return layer[0] # The root of the Merkle tree
# Example usage:
leaves = ["data1", "data2", "data3", "data4", "data5", "data6", "data7", "data8"]
root_hash = merkle_tree(leaves)
print("Merkle tree root hash:", root_hash)
How the Code Works:
- hash_data Function:
- This function takes a string as input and returns its SHA-256 hash.
- It uses the
hashliblibrary to perform the hashing.
- merkle_tree Function:
- Step 1: It first hashes each element of the input data (the
leaveslist) to create the first layer of the tree. - Step 2: The
whileloop iterates as long as the number of elements in thelayeris greater than 1. In each iteration:- If the number of elements is odd, it duplicates the last element to make it even.
- It then hashes each pair of nodes and forms the next layer of the tree.
- Step 3: This process continues until only one element remains in the
layer, which is the Merkle root.
- Step 1: It first hashes each element of the input data (the
Example Breakdown
For the input leaves = ["data1", "data2", "data3", "data4", "data5", "data6", "data7", "data8"], the steps will proceed as follows:
- Initial Layer:
- Hash each element of the leaves list to get the first layer of the tree.
- For example, the first few hashes could look like:
['<hash(data1)>', '<hash(data2)>', ..., '<hash(data8)>'].
- First Iteration:
- Pair up elements of the first layer and hash them to create a new layer. This results in 4 hashes.
- Example pairing:
hash_data(layer[0] + layer[1]), hash_data(layer[2] + layer[3]), ....
- Second Iteration:
- Again, pair up the 4 hashes and create 2 new hashes.
- Third Iteration:
- Pair up the 2 remaining hashes to create a single hash, which is the Merkle root.
Visualizing the Process
In the first iteration, the list comprehension runs 4 times, as there are 8 elements. In the second iteration, it runs 2 times, and in the third, it runs 1 time. This exponential reduction continues until only one hash remains — the Merkle root.
Conclusion
Merkle trees are a powerful tool for verifying data integrity. By hashing data in pairs and recursively building the tree, Merkle trees allow us to efficiently verify large datasets with a single hash at the top — the Merkle root.
By implementing this in Python, you can easily build Merkle trees and use them in applications such as blockchain, distributed systems, or any scenario requiring secure data verification.
How to Run the Code
- Copy the provided Python code.
- Save it in a
.pyfile (e.g.,merkle_tree.py). - Run the file using Python 3:
python merkle_tree.py - The program will output the Merkle tree’s root hash, which represents the entire dataset.

